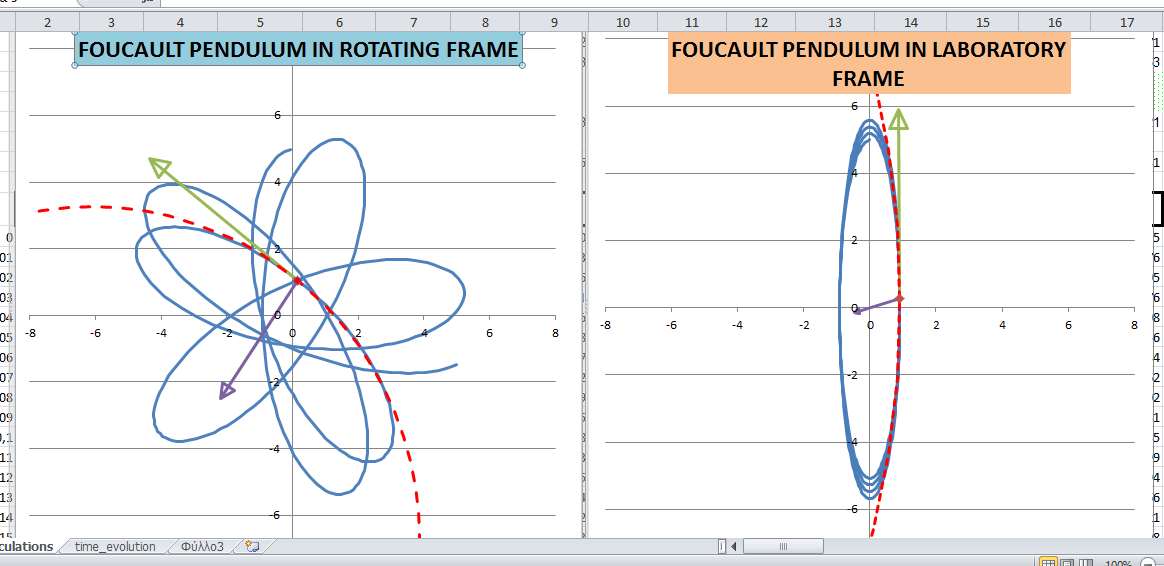
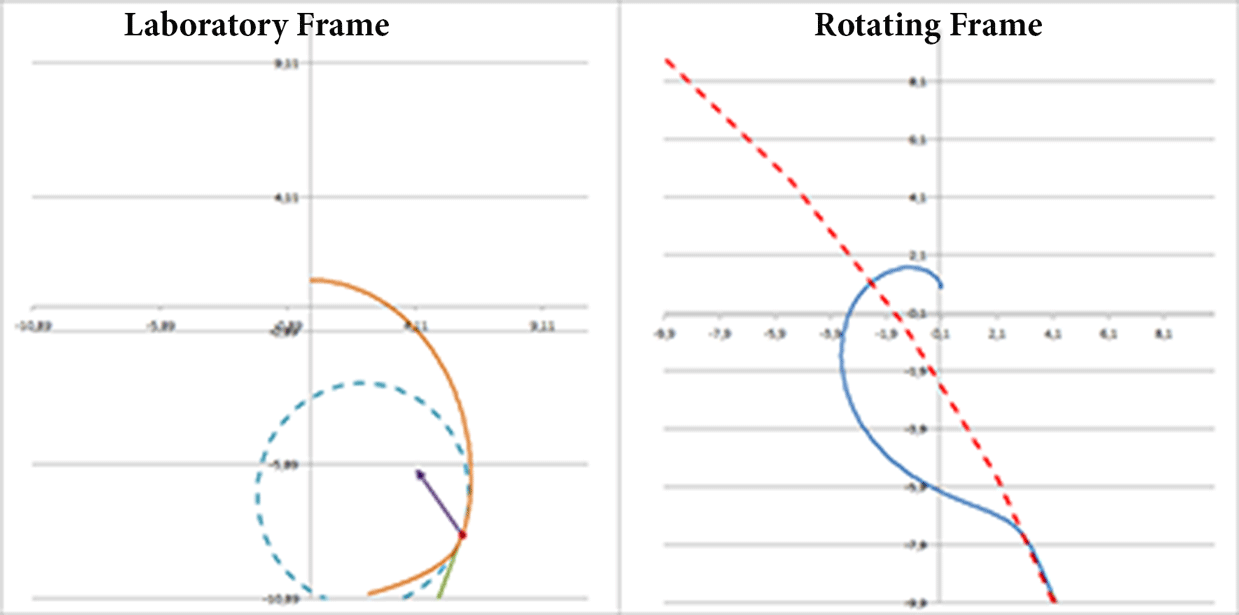
One curve that can be used to introduce students to the ideas of radius of curvature and the relation between angle of velocity and acceleration is the sinusoidal curve.
The length s on the sinusoidal y = B·sinkx is expressed by use of elliptic integrals of the second kind:
where ![]()
A file without macros is available for sinusoidal.

This curve is used by McDermott et al in the Tutorials of introductory physics (2010). This curve is a closed one and shows the change of direction of the centripetal acceleration but also the total acceleration the circle that corresponds to the curvature at the point where the moving body is located. The student can observe that when the body passes through points such as B and C the acceleration is almost tangent to the curve. This curve helps the student to understand that the angle of the acceleration to the velocity is acute when the speed increases and to see that the centripetal acceleration is greatest in the points where the radius of curvature is smallest. The worksheets comes in two forms (with macros, which permit a continuous change) and without, where the body moves by sliding a scroll bar (worksheet tutorial curve.xslx and tutorial curve macros). The points A,…E are points where the student should predict the direction of the acceleration and also draw a circle with a radius equal to the radius of curvature. A file which correspohnds to this curve is TUTORIAL_MACROS. A file without macors is also available

In Neile’s parabola the motion is under the influence of two forces: A horizontal force arising from the reaction of the curve and a vertical force arising from the perpendicular component of the reaction and the weight. For a special value of the initial velocity, its vertical (perpendicular) component remains constant
There is an Excel file "Neile Curve" with macros

In this pendulum the string is constantly in touch with a cycloid. For this pendulum the radius of curvature is studied easily, since it is equal to the length of the string that does not touch the upper curves. The bob of the pendulum describes a cycloid. As the bob approaches the highest point the radius of curvature becomes smaller and eventually it becomes zero. In the case of vibration that starts at this point the velocity is zero and so the centripetal force is zero. This can be contrasted to what happens in Neile curve, At this point the total force (weight) is tangent to the curve.
The student can use the spreadsheet “cycloid pendulum” (with macros or not) to study the motion. The circle of curvature at the highest point has a minimum value which is zero if the bob starts from the cycloid. The student can compare the movement with the simple pendulum and see that the period of the cycloid pendulum is independent of the amplitude of the oscillation.
Motion of a charged body in the combination of a central force field and a magnetic field

We consider a charged body starting with an initial velocity v=vx0 and located at x0=0, y0=R. With ε=qB/m and λ=k/m we have two cases: –ε²+4λ>0 and–ε²+4λ<0 (which holds for a small repulsive force and always for attractive central force)
In this case we have an oscillatory motion. There is a flie with mcacros that can be downloaded amd also a file without macros.