AL HAYTHAM'S PROBLEM

We present here: 1st Lemma, 3rd Lemma, 4th Lemma Use of 4th Lemma to solve the problem, Huygens' solution, Numerical Solution to Al Haytham's problem , Hyperbola, Ellipse

Al Haytham's problem concerns the number of points that can join in a sphere 2 other  points through refraction.

In the figure A: source, B: eye, P: point of reflection. First cut: region of the circle contained in the acute angle APB, opposite cut: the symmetric  part of the surface through C.

Al Haytham proved that the highest number of points that can join A and B are four. His proof is based on lemmas described in Sabra's work: Ibn Al Haytham's lemmas for solving "AlHazens'" problem (Archive for the Exact Sciences Vol. 26 December 1982)

Software was developed to have an interactive way of following the construction and the proof of the lemmas.

To find the 4 points we use the 4th lemma. This lemma in turn uses the 3rd lemma which in turn uses the 1s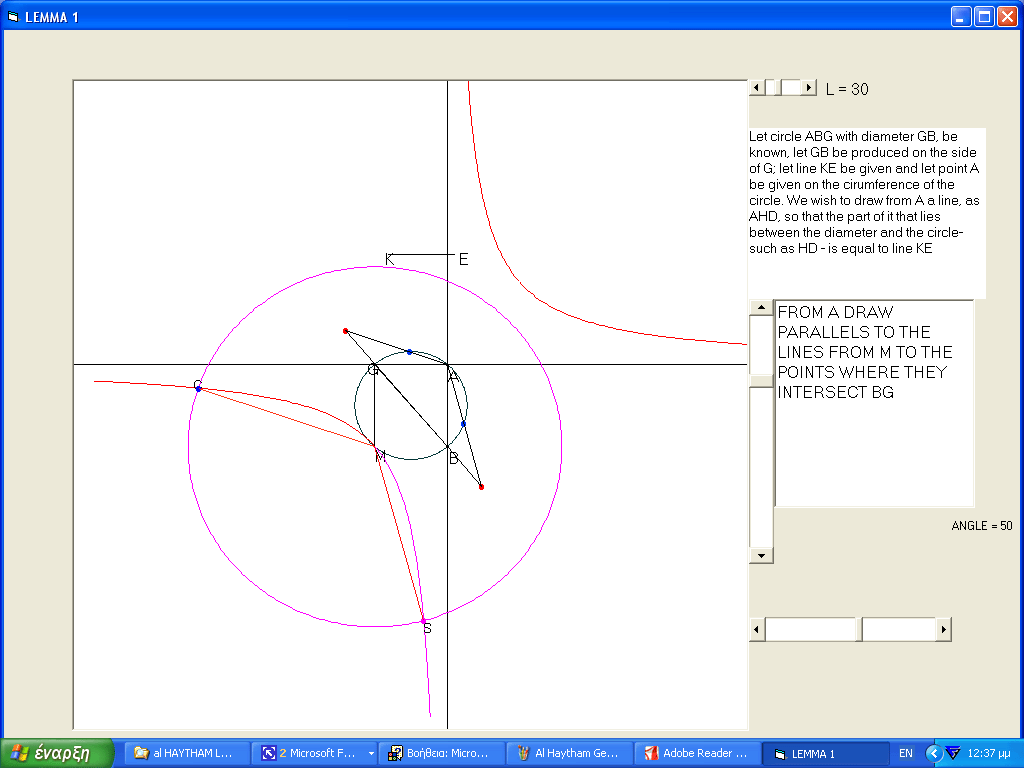t or second.

1st lemma:  An excel file was developed: AL HAYTHAM'S FIRST LEMMA

Let circle ABG , with diameter GB, be known ; let GB be produced the side of G; let line KE be given and let point A be given on the circumference of the circle. We wish to draw from A a line, as AHD, so that the part of it that lies between the diameter and the circle--such as HD--is equal to line KE.

The second lemma is similar to the first

The 3rd lemma can be downloaded from LEMMA_3.exe An Excel file fro 3rd Lemma INDEX FILES/LEMMA 3.xlsx There are instructions for al Haytham Lemmas

Third lemma:

Again, in triangle ABG let angle B be right; let D be given on line BG; and let the ratio of E to Z be known; we wish to draw from D a line like DTK so that the ratio of TK to TG is as the ratio of E to Z.

The 3rd lemma uses the 1st lemma in constructing

The proof is given in 9 steps.

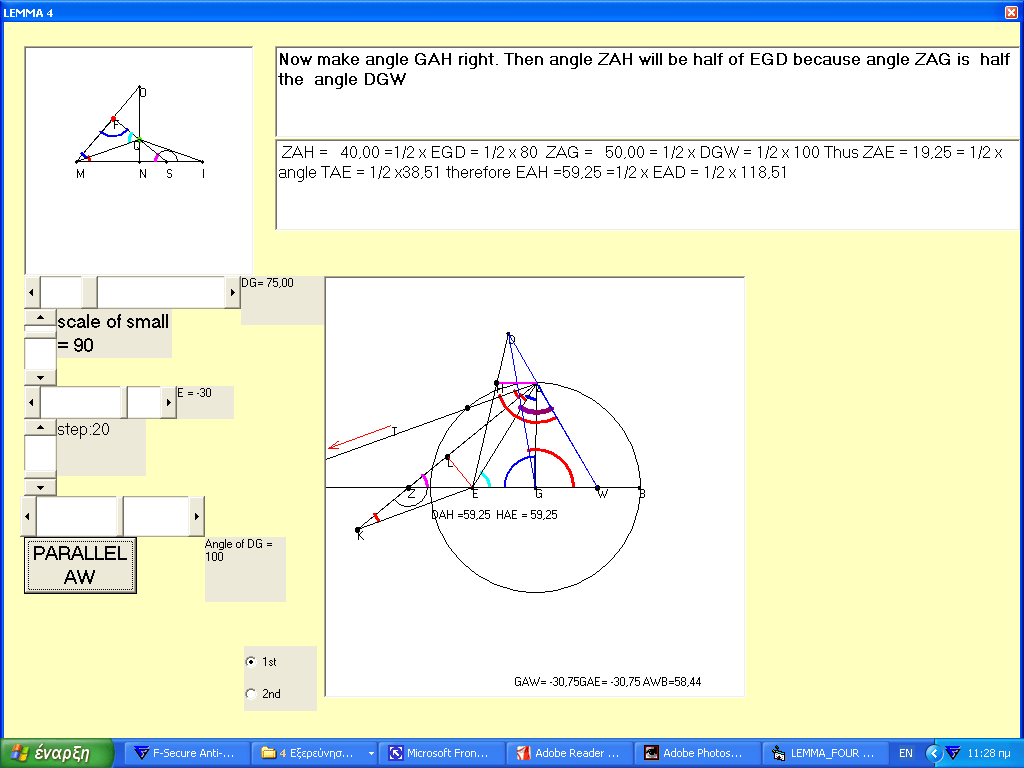
Fourth Lemma: This Lemma is used to find the points on the circle that solve the problem.
We present two software applications:

1) proof LEMMA 4 HAYTHAM.exe An excel file with 15 steps is Proof of 4th Lemma INDEX FILES/LEMMA 4.xlsx

This is a difficult proof with 20 steps. The picture shows the final step:

On the left side we see the use of the 3rd lemma.

In the 1st text box we have explanations of what is involved on each step.

On the 2nd text box we have the calculations of several parameters that are connected with each step.

On the 20th step it appears the button PARALLEL AW, which deals with a special case.

2) We use the lemma with the software application LEMMA 4 HAYTHAM.exe4TH LEMMA

  An Excel file for the use of the 4th Lemma INDEX FILES/USE OF LEMMA 4.xlsx

This screen shows on the left side the use of 3rd lemma.

HUYGENS' SOLUTION TO AL HAYTHAM'S PROBLEM 1672 solution and 1665 solution

On the left is presentedHuygens

'

solution (which is based on Analytic Geometry and use of Appolonius circle based)

A  numerical solution can be found by using EXCEL

The points (rectangles) are joined here by 4 points. The user can see that by changing the angle, he can get  4 or 2 points on the circle.

Using the EXCEL file we can see that the points that connect the rectangles the path of light has an extremum (a maximum or a minimum)

We can compare the circle with the case of parabola or ellipse

Here as we check for the total path we can see a) For parabola all the paths that start at a certain distance Y from the X-axis have the same path and that the reflected ray passes through the focus of the parabola

b) For the ellipse we can see that all the rays starting from one focus pass through the other focus after the reflection and that the pat is the same for all rays (basic property of ellipses)

Free Counter